Конспект по биологии на тему «Состав и функции крови» (8 класс).

ПЛА́ЗМА (греч. πλάσμα – вы­ле­п­лен­ное, оформ­лен­ное), ио­ни­зо­ван­ный газ, со­стоя­щий из элек­тро­нов и ио­нов, дви­же­ние ко­то­рых оп­ре­де­ля­ет­ся пре­им. кол­лек­тив­ным ха­рак­те­ром взаи­мо­дей­ст­вия за счёт даль­но­дей­ст­вую­щих элек­тро­маг­нит­ных сил, в от­ли­чие от обыч­но­го га­за, в ко­то­ром до­ми­ни­ру­ют близ­ко­дей­ст­вую­щие пар­ные взаи­мо­дей­ст­вия (столк­но­ве­ния). Вы­со­кая элек­тро­про­вод­ность П. де­ла­ет её чув­ст­ви­тель­ной к воз­дей­ст­вию элек­тро­маг­нит­ных по­лей. Спе­ци­фи­ка от­кли­ка П. на та­кое воз­дей­ст­вие по­зво­ля­ет счи­тать П. осо­бым (чет­вёр­тым) аг­ре­гат­ным со­стоя­ни­ем ве­ще­ст­ва на­ря­ду с твёр­дым те­лом, жид­ко­стью и га­зом.

Основные параметры и свойства плазмы

Ко­ли­че­ст­вен­но П. ха­рак­те­ри­зу­ет­ся кон­цен­тра­ция­ми элек­тро­нов $n_e$ и ио­нов $n_i$, их ср. темп-ра­ми (энер­гия­ми) $T_e$ и $T_i$, сте­пе­нью ио­ни­за­ции (дóлей ио­ни­зо­ван­ных ато­мов) $α=n_i/(n_i+n_0)$, где $n_0$ – кон­цен­тра­ция ней­траль­ных ато­мов, ср. за­ря­дом ио­на $Z_{eff}$. Вы­со­кая под­виж­ность час­тиц П. (осо­бен­но элек­тро­нов) обес­пе­чи­ва­ет эк­ра­ни­ро­ва­ние вне­сён­но­го в П. за­ря­да на рас­стоя­ни­ях по­ряд­ка де­ба­евско­го ра­диу­са эк­ра­ни­ро­ва­ния $r_D$ за вре­ме­на по­ряд­ка об­рат­ной плаз­мен­ной элек­трон­ной (лен­гмю­ров­ской) час­то­ты , $ω_{ре}=\sqrt{4πn_ee^2/m_e},$ где $e$ и $m_e$ – за­ряд и мас­са элек­тро­на; здесь и ни­же в фор­му­лах ис­поль­зу­ет­ся га­ус­со­ва сис­те­ма еди­ниц (СГС); темп-ру в фи­зи­ке П. при­ня­то из­ме­рять в энер­ге­тич. еди­ни­цах (1 кэВ≈107 К). Про­стран­ст­вен­ный и вре­мен­нoй мас­шта­бы обыч­но ма­лы, по­это­му кон­цен­тра­ции по­ло­жи­тель­ных и от­ри­ца­тель­ных за­ря­дов ока­зы­ва­ют­ся прак­ти­че­ски оди­на­ко­вы­ми $(|Z_{eff}n_i-n_e|/n_e≪1)$; в этом смыс­ле го­во­рят о ква­зи­нейт­раль­но­сти П. Это важ­ней­шее свой­ство П. час­то ис­поль­зу­ют для оп­ре­де­ле­ния П., сле­дуя И. Лен­гмю­ру, впер­вые при­ме­нив­ше­му в 1920-х гг. тер­мин «П.» для обо­зна­че­ния уда­лён­ной от элек­тро­дов ква­зи­нейт­раль­ной об­лас­ти га­зо­во­го раз­ря­да. Обыч­но вре­ме­на су­ще­ст­во­ва­ния и раз­ме­ры П. пре­вы­ша­ют со­от­вет­ст­вен­но и $r_D$, что обес­пе­чи­ва­ет её ква­зи­нейт­раль­ность. Ква­зи­нейт­раль­ность П. не про­ти­во­ре­чит на­ли­чию объ­ём­но­го элек­трич. по­ля в П., на­хо­дя­щей­ся в маг­нит­ном по­ле.

Классификация видов плазмы

Клас­си­фи­ка­ция ви­дов плаз­мы ус­ловна. Ес­ли в сфе­ре ра­диу­са $r_D$ на­хо­дит­ся мно­го за­ря­жен­ных час­тиц ($N≈4πnr_D^3/3≫1, n$ – кон­цент­ра­ция всех ча­стиц плаз­мы), П. на­зы­ва­ет­ся иде­аль­ной плаз­мой; при $N⩽1$ го­во­рят о не­иде­аль­ной плаз­ме (здесь $N$ – па­ра­метр иде­аль­но­сти). В иде­аль­ной П. по­тен­ци­аль­ная энер­гия взаи­мо­дей­ст­вия час­тиц ма­ла по срав­не­нию с их те­п­ло­вой энер­ги­ей.

Вы­со­ко­ио­ни­зо­ван­ную П. с темп-рой $⩾10^2–10^3$ эВ на­зы­ва­ют вы­со­ко­тем­пе­ра­тур­ной, в от­ли­чие от низ­ко­тем­пе­ра­тур­ной плаз­мы с $T_e⩽10–100$ эВ, в ко­то­рой су­ще­ст­вен­ную роль мо­гут иг­рать столк­но­ви­тель­ные и ра­диа­ци­он­ные про­цес­сы. Осо­бой раз­но­вид­но­стью низ­ко­тем­пе­ра­тур­ной П. яв­ля­ет­ся пы­ле­вая плаз­ма, со­дер­жа­щая мак­ро­ско­пи­че­ские (раз­ме­ром от до­лей до со­тен мик­ро­мет­ров) твёр­дые час­тич­ки, не­су­щие боль­шой элек­трич. за­ряд $(Z_{eff}≫1)$. Вы­со­ко­тем­пе­ра­тур­ную П. с вы­со­кой элек­тро­про­вод­но­стью $σ$ так­же на­зы­ва­ют иде­аль­ной, ес­ли мож­но пре­неб­речь дис­си­па­тив­ны­ми про­цес­са­ми.

При сверх­вы­со­ких плот­но­стях энер­гии, воз­ни­каю­щих в ре­зуль­та­те столк­но­ве­ний тя­жё­лых ульт­ра­ре­ля­ти­ви­ст­ских час­тиц, воз­мож­но об­ра­зо­ва­ние кварк-глю­он­ной плаз­мы – ад­рон­ной сре­ды, в ко­то­рой пе­ре­ме­ша­ны цвет­ные за­ря­ды квар­ков и глюо­нов, как в обыч­ной П. пе­ре­ме­ша­ны элек­трич. за­ря­ды. Час­ти­цы крио­ген­ной плаз­мы (с темп-рой в до­ли кель­ви­на) соз­да­ют­ся пу­тём пре­ци­зи­он­ной ио­ни­за­ции хо­лод­ных ато­мов ла­зер­ным пуч­ком, энер­гия кван­тов ко­то­ро­го прак­ти­че­ски рав­на энер­гии ио­ни­за­ции. Для опи­са­ния элек­тро­нов в ме­тал­лах, за­ряд ко­то­рых ском­пен­си­ро­ван за­ря­дом ио­нов кри­стал­лич. ре­шёт­ки, а так­же элек­тро­нов и ды­рок в по­лу­про­вод­ни­ках час­то ис­поль­зу­ют тер­мин плаз­ма твёр­дых тел. Совр. фи­зи­ка П. рас­смат­ри­ва­ет так­же ла­зер­ную плаз­му, воз­ни­каю­щую при оп­ти­че­ском про­бое под дей­ст­ви­ем мощ­но­го ла­зер­но­го из­лу­че­ния на ве­ще­ст­во; за­ря­жен­ную П., в ча­ст­но­сти элек­трон­ные и ион­ные пуч­ки, за­ря­жен­ные слои (двой­ной элек­три­че­ский слой) и др.

П. на­зы­ва­ют вы­ро­ж­ден­ной при низ­кой темп-ре $T$ и вы­со­кой кон­цен­тра­ции час­тиц $n$, ко­гда ха­рак­тер­ное рас­стоя­ние $(∝n^{–1/3})$ ме­ж­ду ни­ми ста­но­вит­ся по­ряд­ка дли­ны вол­ны де Брой­ля $(λ≈h/(2mT)^{1/2}$, где $h$ – по­сто­ян­ная План­ка). Ис­кус­ст­вен­но соз­дан­ная П. обыч­но тер­мо­ди­на­ми­че­ски не­рав­но­вес­на. Ло­каль­ное рав­но­ве­сие на­сту­па­ет, толь­ко ес­ли час­ти­цы П. стал­ки­ва­ют­ся ме­ж­ду со­бой. Бы­ст­рее все­го ус­та­нав­ли­ва­ет­ся рав­но­ве­сие внут­ри элек­трон­ной ком­по­нен­ты П., а в ион­ной ком­по­нен­те и ме­ж­ду ио­на­ми и элек­тро­на­ми – со­от­вет­ст­вен­но в $\sqrt{∼m_i/m_e}$ и $∼m_i/m_e$ раз мед­лен­нее. В от­ли­чие от га­за, час­то­та столк­но­ве­ний час­тиц П. умень­ша­ет­ся с уве­ли­че­ни­ем энер­гии час­тиц ($∝T^{–3/2}$). По чис­лу ви­дов ио­нов раз­ли­ча­ют од­но- и мно­го­ком­по­нент­ную плаз­му.

Плазма в природе и технике

Счи­та­ет­ся, что бо­лее 99% ба­ри­он­но­го ве­ще­ст­ва во Все­лен­ной пре­бы­ва­ет в со­стоя­нии П. в ви­де звёзд, меж­звёзд­но­го и меж­га­лак­тич. га­за (см. Кос­ми­че­ская плаз­ма). П. маг­ни­то­сфе­ры за­щи­ща­ет Зем­лю от раз­ру­ши­тель­но­го по­то­ка П., ис­пус­кае­мой Солн­цем, – сол­неч­но­го вет­ра. При­сут­ст­вие ио­но­сфер­ной П., от­ра­жаю­щей ра­дио­вол­ны, де­ла­ет воз­мож­ной даль­нюю ра­дио­связь. П. в при­ро­де мож­но на­блю­дать в ви­де ат­мо­сфер­ных раз­ря­дов (мол­ний и ко­рон­ных раз­ря­дов) и по­ляр­ных сия­ний, а так­же в обыч­ном пла­ме­ни. В тех­ни­ке наи­боль­шее рас­про­стра­не­ние по­лу­чи­ла П. га­зо­вых раз­ря­дов, ис­поль­зуе­мых в ла­бо­ра­тор­ных и тех­но­ло­гич. це­лях, в га­зо­раз­ряд­ных ис­точ­ни­ках све­та (напр., лю­ми­нес­цент­ных лам­пах), в ком­му­ти­рую­щих уст­рой­ст­вах, при свар­ке и рез­ке ма­те­риа­лов, в плаз­мен­ных па­не­лях те­ле­ви­зи­он­ных и муль­ти­ме­дий­ных эк­ра­нов. По­то­ки П. при­ме­ня­ют­ся в плаз­мо­тро­нах для об­ра­бот­ки ма­те­риа­лов, в хи­рур­гии, в плаз­мен­ных кос­мич. дви­га­те­лях и маг­ни­то­гид­ро­ди­на­ми­че­ских ге­не­ра­то­рах. В вы­со­ко­тем­пе­ра­тур­ной П. воз­мож­но про­те­ка­ние тер­мо­ядер­ных ре­ак­ций. Для реа­ли­за­ции управ­ляе­мо­го тер­мо­ядер­но­го син­те­за (УТС) в дей­те­рий-три­тие­вой П. не­об­хо­ди­мо вы­пол­не­ние Ло­усо­на кри­те­рия – удер­жа­ние П. с $T⩾10$ кэВ и $n⩾10^{14}$ см–3 в те­че­ние вре­ме­ни $⩾1$ с (в П. др. со­ста­ва эти зна­чения ещё вы­ше). Ти­пич­ные зна­че­ния па­ра­мет­ров разл. ви­дов плаз­мы при­ве­де­ны на ри­сун­ке.

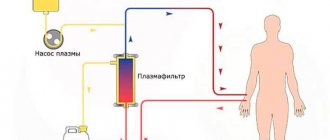
Вязкость

Вязкость крови – способность её сопротивляться течению жидкости во время перемещения частиц с помощью внутреннего трения. С одной стороны, это сложные взаимоотношения между макромолекулами коллоидов и водой, с другой – между форменными элементами и плазмой. Вязкость плазмы выше, чем у воды. Чем больше она содержит крупномолекулярных белков (липопротеинов, фибриногена), тем сильнее вязкость плазмы. В целом данное свойство крови отражается на общем периферическом сосудистом сопротивлении кровотоку, то есть обусловливает функционирование сердца и сосудов.

Методы описания плазмы

Области значений параметров различных видов плазмы. Прямые линии разграничивают области идеальной и неидеальной плазмы (параметр идеальности N=1), области классической и вырожденной плазмы (Т=ℰF, ℰF –…

Ес­те­ст­вен­ный спо­соб опи­сать П., про­ве­дя рас­чёт дви­же­ния всех её час­тиц, не реа­ли­зу­ем на прак­ти­ке да­же с по­мо­щью мощ­ной вы­чис­лит. тех­ни­ки в си­лу кол­лек­тив­но­го ха­рак­те­ра взаи­мо­дей­ст­вия час­тиц. Од­на­ко мн. важ­ные свой­ст­ва П. мож­но по­нять на ос­но­ве ана­ли­за дви­же­ния отд. час­тиц. В маг­нит­ном по­ле с ин­дук­ци­ей $\boldsymbol B$ дви­же­ние за­ря­жен­ных час­тиц П. вдоль и по­пе­рёк на­прав­ле­ния маг­нит­но­го по­ля су­ще­ст­вен­но раз­лич­но. В про­доль­ном на­прав­ле­нии час­ти­ца с за­ря­дом $q$ дви­жет­ся по­сту­па­тель­но, а в по­пе­реч­ном – вра­ща­ет­ся с цик­ло­трон­ной час­то­той $ω_B=qB/mc$ ($c$ – ско­рость све­та). Ес­ли лар­мо­ров­ский ра­ди­ус $ρ_L=v_⟂/ω_B$ та­ко­го вра­ще­ния мень­ше дли­ны сво­бод­но­го про­бе­га час­ти­цы и ха­рак­тер­но­го раз­ме­ра П., а элек­тро­маг­нит­ное по­ле ме­ня­ет­ся мед­лен­но по срав­не­нию с пе­рио­дом цик­ло­трон­но­го вра­ще­ния, П. счи­та­ет­ся за­маг­ни­чен­ной плаз­мой ($v_⟂$ – ско­рость дви­же­ния час­ти­цы по­пе­рёк маг­нит­но­го по­ля). Час­ти­цы та­кой П. дви­жут­ся с со­хра­не­ни­ем адиа­ба­тич. ин­ва­ри­ан­та – маг­нит­но­го мо­мен­та $μ \approx mv_⟂^2/2B$, а под дей­ст­ви­ем к.-л. си­лы $\boldsymbol F$ опи­сы­вае­мые ими лар­мо­ров­ские спи­ра­ли мед­лен­но дрей­фу­ют по­пе­рёк маг­нит­но­го по­ля со ско­ро­стью $\boldsymbol v_F=c[\boldsymbol F×\boldsymbol B]/qB^2$. В за­ви­си­мо­сти от при­ро­ды си­лы $\boldsymbol F$ раз­ли­ча­ют гра­ви­та­ци­он­ный, элек­три­че­ский, гра­ди­ент­ный, цен­тро­беж­ный и по­ля­ри­за­ци­он­ный дрей­фы (см. Дрейф за­ря­жен­ных час­тиц). На­прав­ле­ние цик­ло­трон­но­го вра­ще­ния час­тиц оп­ре­де­ля­ет­ся Лен­ца пра­ви­лом: маг­нит­ное по­ле то­ка цик­ло­трон­но­го вра­ще­ния час­тиц про­ти­во­по­лож­но внеш­не­му по­лю и, сле­до­ва­тель­но, ос­лаб­ля­ет его. В этом про­яв­ля­ет­ся диа­маг­не­тизм П., при­во­дя­щий к вы­тал­ки­ва­нию П. из об­лас­ти бо­лее силь­но­го маг­нит­но­го по­ля.

То­ж­де­ст­вен­ность час­тиц ка­ж­дой ком­по­нен­ты П. по­зво­ля­ет ис­поль­зо­вать ки­не­тич. опи­са­ние с по­мо­щью од­но­час­тич­ной функ­ции рас­пре­де­ле­ния $f(t, \boldsymbol r, \boldsymbol v)$, оп­ре­де­ляе­мой как кон­цен­тра­ция час­тиц дан­ной ком­по­нен­ты в фа­зо­вом про­стран­ст­ве (см. Ки­не­ти­че­ские урав­не­ния для плаз­мы). Как и обыч­ная кон­цен­тра­ция, функ­ция рас­пре­де­ле­ния удов­ле­тво­ря­ет урав­не­нию не­пре­рыв­но­сти, но толь­ко в фа­зо­вом про­стран­ст­ве: $